Geogebra

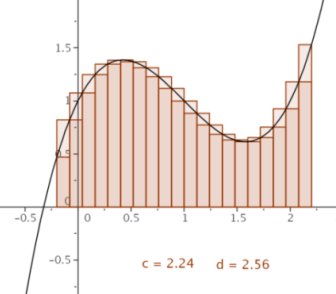
Ecco un esempio di che cosa si può fare con Geogebra: il grafico mostra le somme inferiori e superiori per arrivare al concetto di integrale definito.

Qui trovate la schermata iniziale di Geogebra e qui il link al sito da cui è possibile scaricare il sofrware.

Come si può vedere è disponibile sotto licenza GPL anche in ambiente Windows.

Esiste anche un forum in italiano: per accedere clicca qui

E’ un pacchetto che riunisce in sè molte delle potenzialità di noti software commerciali, (alludo a Cabrì ed a Derive) unendo l’aspetto geometrico a quello algebrico.

Il suo uso è molto intuitivo. Lo schermo è, di default, diviso in due zone: a destra compaiono tutti gli oggetti geometrici, a sinistra le loro coordinate o equazionidinamicamente collegati e con la chiara distinzione tra oggetti indipendenti ed oggetti dipendenti. Il collegamento dinamico fà sì che ogni cambiamento effettuato da una parte si ripercuote in tempo reale dall’altra.

Nella parte alta si trovano le icone di una serie di menu in basso la linea di immissione dei comandi a sinistra una finestra (che si può chiudere) con l’espressione algebrica di tutti gli oggetti presenti nella finestra di destra.

E’ possibile sia esportare i fogli di lavoro dinamici e /o le pagine in cui sono indicate le costruzioni in formato html come pagine web, e quindi condividere sia le figure come immagini in vari formati tra cui .pmg e .eps. inseribili quindi facilmente in un documento di TeX. A questo proposito mi piace segnalare che Geogebra accetta la sintasssi TeX per tutte le formule, anche quelle inserite nel foglio da disegno.

Vediamo due possibili semplici esempi didattici:

Studio di una conica: è data la conica di equazione ax^2+bxy+cy^2+dx+ey+f=0; si possono far variare indipendentemente e con continuità i sei coefficienti agendo sui cursori ed osservare come varia la conica.

Integrale definito: calcola l’integrale definito da a a b di f(x): divide l’intervallo in n parti e calcola le somme inferiori le somme superiori e l’integrale. Variando con il cursore il numero n degli intervalli si vede bene l’approssimazione; in basso compaiono i valori dell’integrale e le sue approssimazioni per difetto e per eccesso aggiornate in tempo reale.

Altre applicazioni le potete trovare qui.

N.B. Se le applicazioni non partono o non si animano è probabile che sul tuo PC non sia installata la JVM (Java Virtual Machine); in tal caso puoi provvedere cliccando qui.